데이터 상세
공무원연금공단_지역별 가입자 추이
공무원연금공단에서 관리하는 공무원연금 가입자 수의 연도별 변화를 지역별로 구분하여 집계한 데이터로, 전국 17개 광역자치단체를 기준으로 가입자 수의 장기적 추이를 제공합니다.
제공 지역에는 서울, 부산, 대구, 인천, 광주, 대전, 세종, 울산, 경기, 강원, 충북, 충남, 경북, 경남, 전북, 전남, 제주가 포함되며, 각 연도별 총 가입자 수와 지역별 세부 가입자 수가 포함되어 있습니다.
이 데이터는 1982년부터 기준년도까지 시계열로 구성되어 있어, 특정 지역에서의 공무원 규모 변화, 인사 정책의 효과, 지역별 인력 밀집도 변화 등을 파악하는데 활용될 수 있습니다.
제공 지역에는 서울, 부산, 대구, 인천, 광주, 대전, 세종, 울산, 경기, 강원, 충북, 충남, 경북, 경남, 전북, 전남, 제주가 포함되며, 각 연도별 총 가입자 수와 지역별 세부 가입자 수가 포함되어 있습니다.
이 데이터는 1982년부터 기준년도까지 시계열로 구성되어 있어, 특정 지역에서의 공무원 규모 변화, 인사 정책의 효과, 지역별 인력 밀집도 변화 등을 파악하는데 활용될 수 있습니다.
공공데이터활용지원센터는 공공데이터포털에 개방되는 3단계 이상의 오픈 포맷 파일데이터를 오픈 API(RestAPI 기반의 JSON/XML)로 자동변환하여 제공합니다.
오픈 API를 활용하기 위해서는 공공데이터포털 회원 가입 및 활용신청이 필요하며, 활용 관련 문의는 공공데이터활용지원센터로 연락주시기 바라며,
데이터 자체에 대한 문의는 아래 제공기관의 관리부서 전화번호로 연락주시기 바랍니다.
파일데이터는 로그인 없이 다운로드를 통해 이용하실 수 있습니다.
오픈 API를 활용하기 위해서는 공공데이터포털 회원 가입 및 활용신청이 필요하며, 활용 관련 문의는 공공데이터활용지원센터로 연락주시기 바라며,
데이터 자체에 대한 문의는 아래 제공기관의 관리부서 전화번호로 연락주시기 바랍니다.
파일데이터는 로그인 없이 다운로드를 통해 이용하실 수 있습니다.
다른 사용자들이 활용한 데이터
로그인하셔서 다른 사용자들이 활용한 데이터를 추천받아 보세요
파일데이터 정보
공공데이터활용지원센터는 공공데이터포털에 개방되는 3단계 이상의 오픈 포맷 파일데이터를 오픈 API(RestAPI 기반의 JSON/XML)로 자동변환하여 제공합니다.
오픈 API를 활용하기 위해서는 공공데이터포털 회원 가입 및 활용신청이 필요하며, 활용 관련 문의는 공공데이터활용지원센터로 연락주시기 바랍니다.
파일데이터는 로그인 없이 다운로드를 통해 이용하실 수 있습니다.
오픈 API를 활용하기 위해서는 공공데이터포털 회원 가입 및 활용신청이 필요하며, 활용 관련 문의는 공공데이터활용지원센터로 연락주시기 바랍니다.
파일데이터는 로그인 없이 다운로드를 통해 이용하실 수 있습니다.
다른 사용자들이 활용한 데이터
로그인하셔서 다른 사용자들이 활용한 데이터를 추천받아 보세요
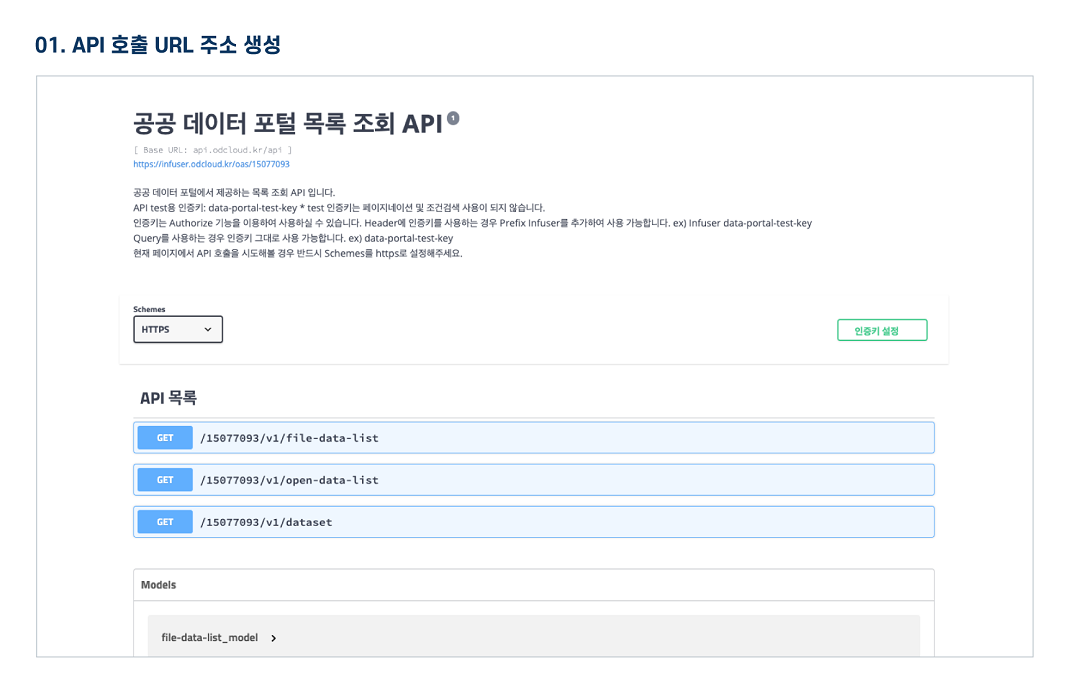
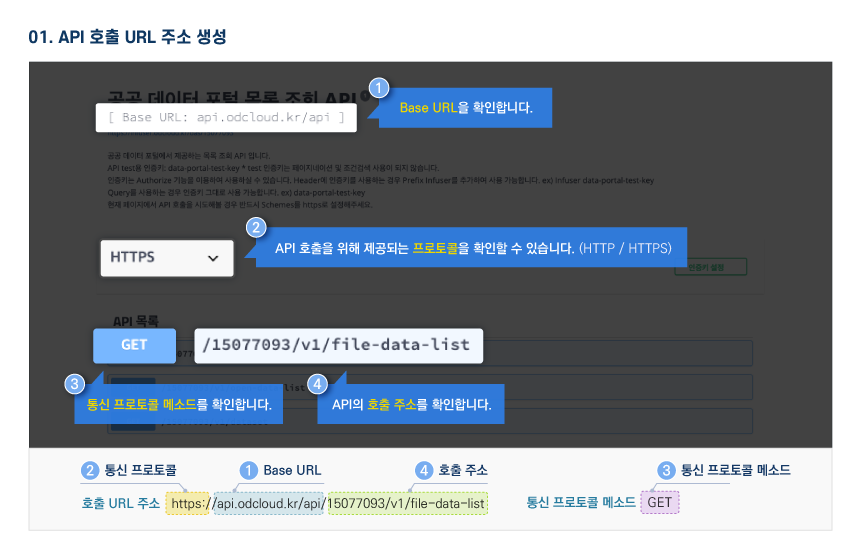
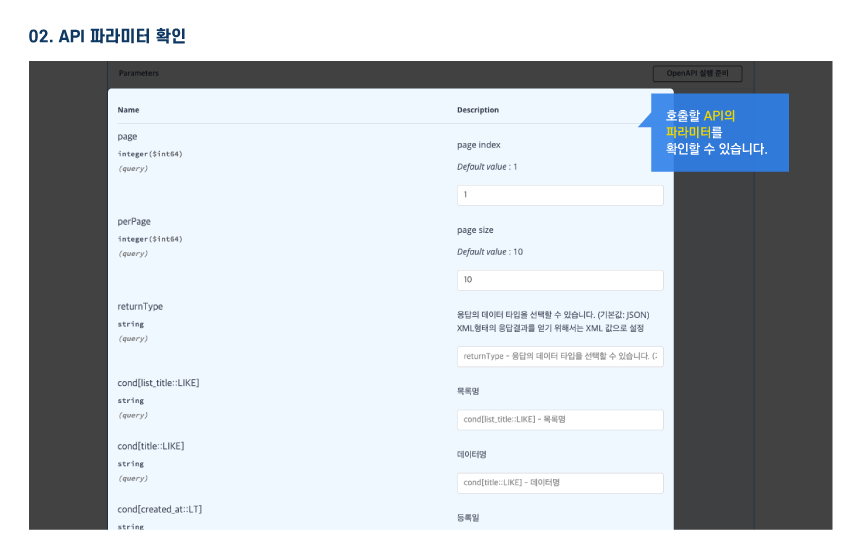
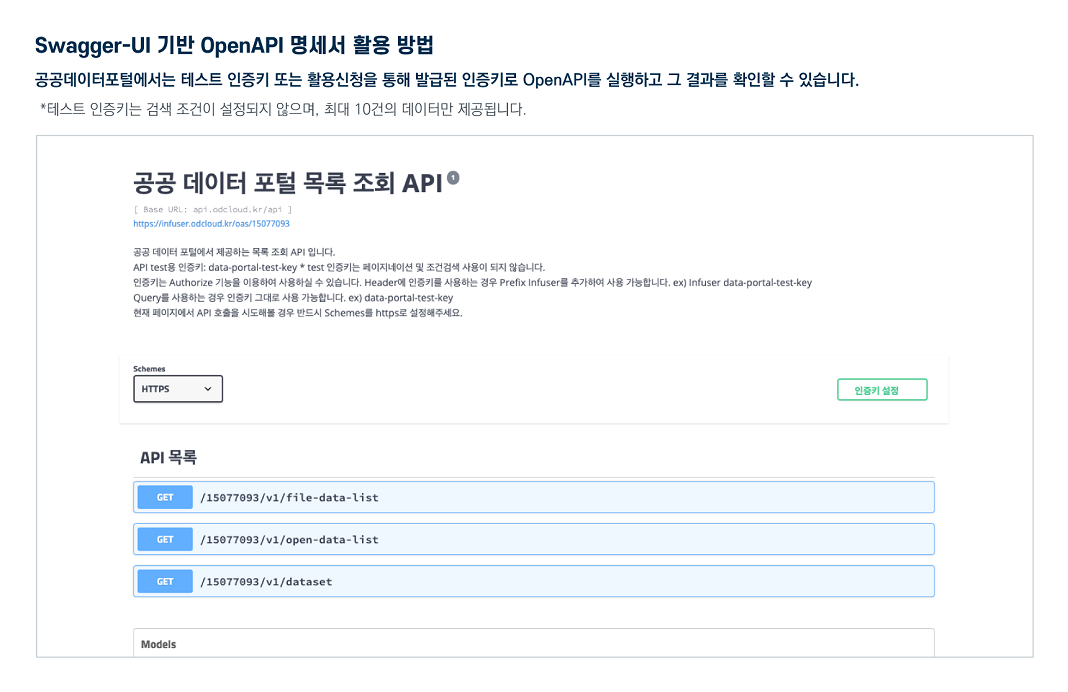
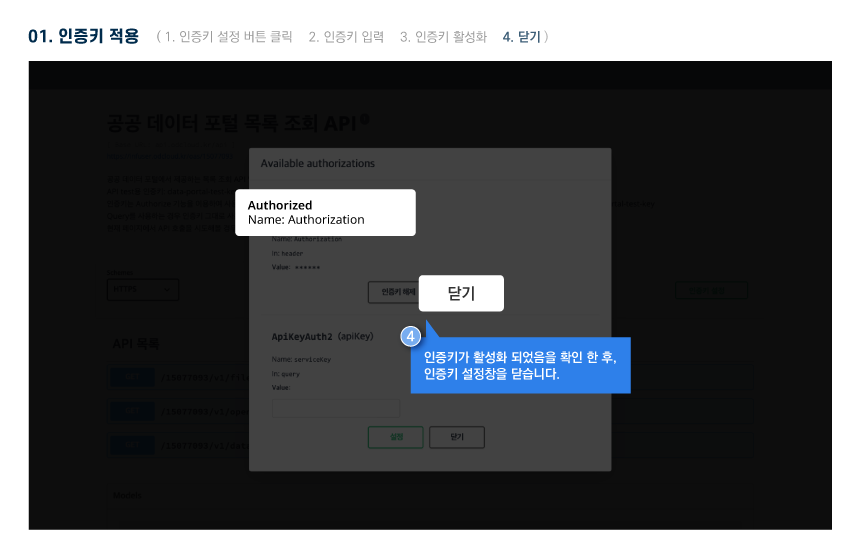
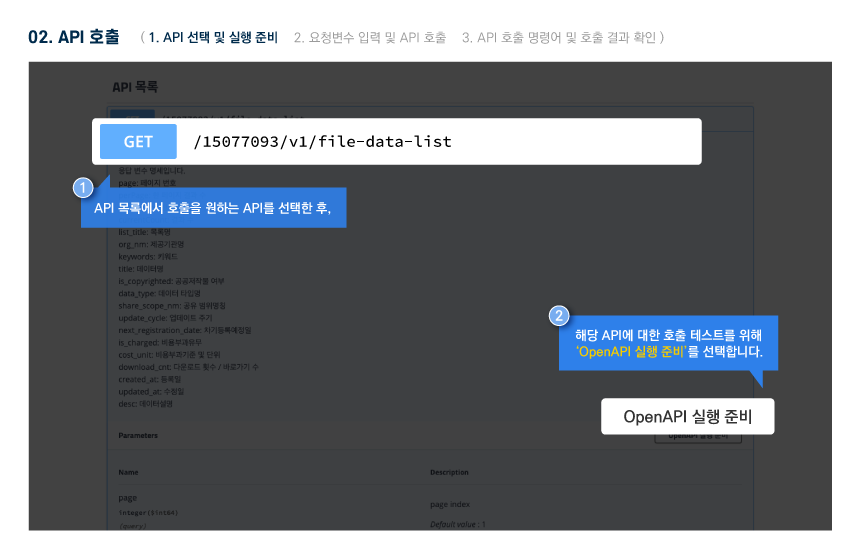
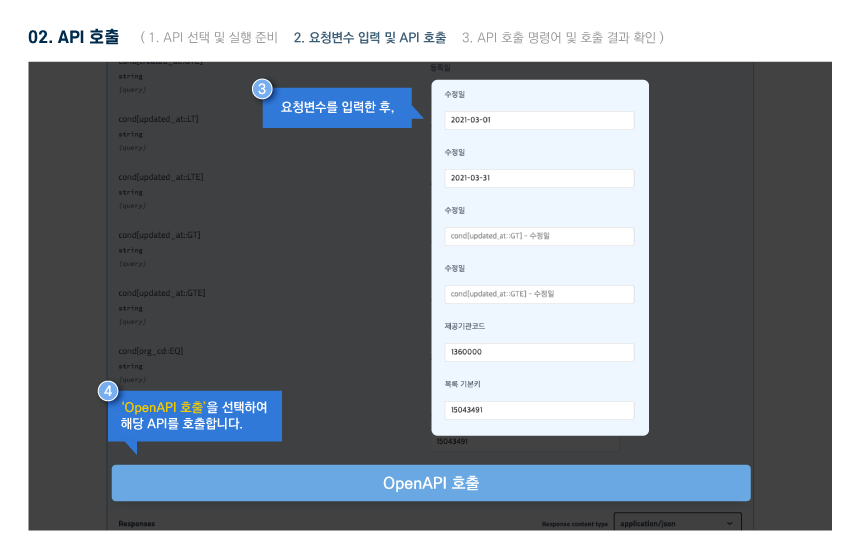
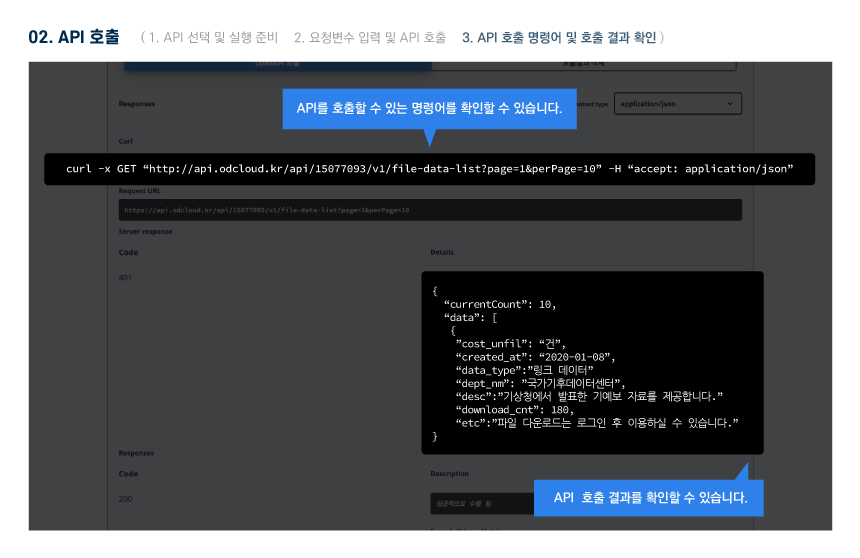
오픈API 정보
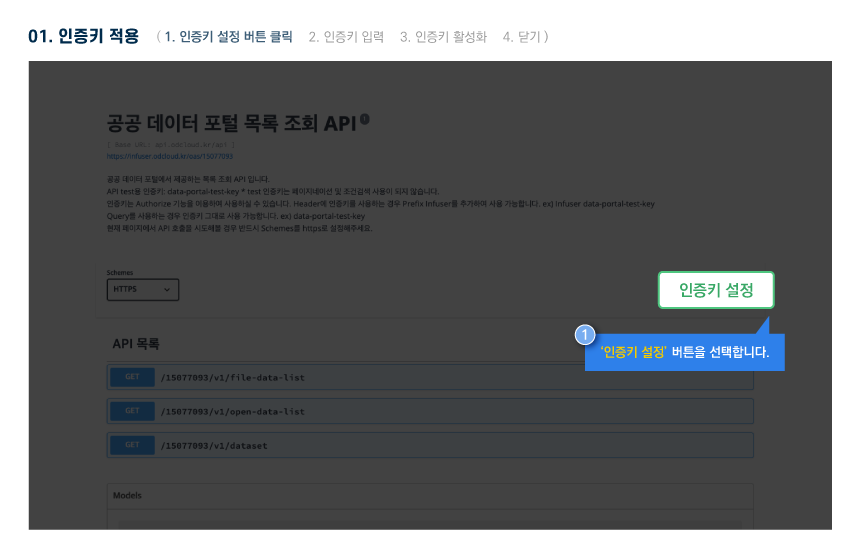
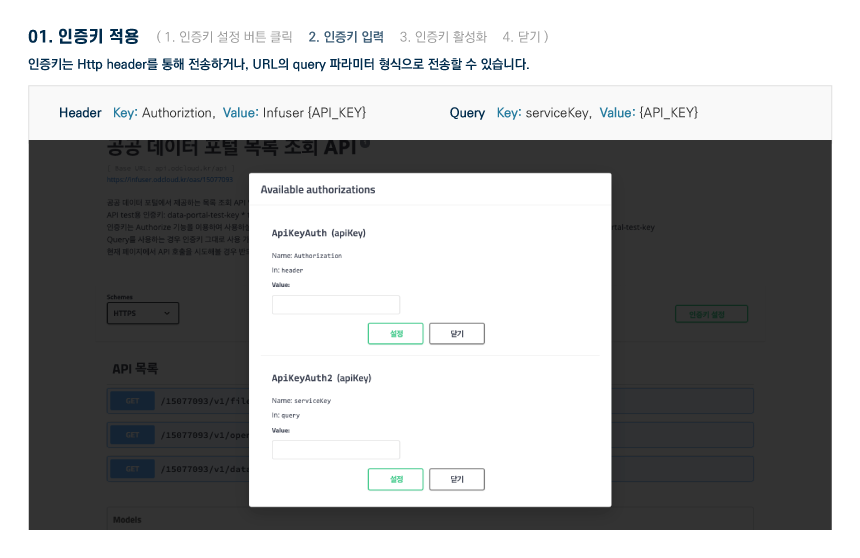
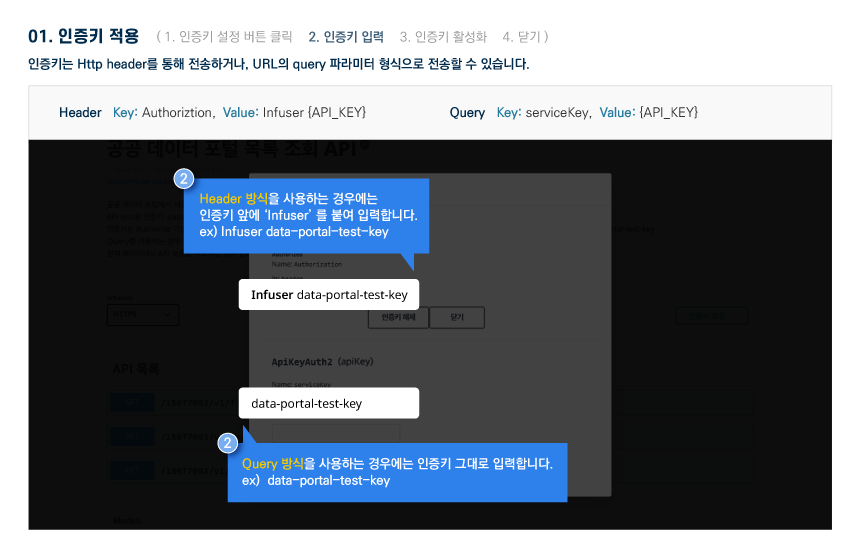
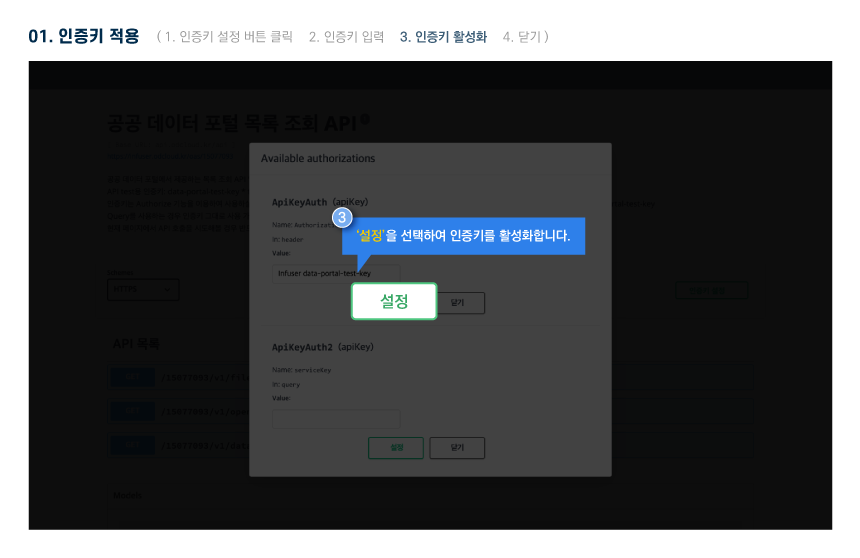
활용 명세
Open API 명세 확인 가이드
다른 사용자들이 활용한 데이터
로그인하셔서 다른 사용자들이 활용한 데이터를 추천받아 보세요
이 데이터와 유사한 데이터